densematrixmodule Module Reference

Module with subroutines for solution of dense linear equation systems. More...

Data Types
interface	solveeigenvalues
	Solves an eigenvalue problem. More...

Functions/Subroutines
subroutine	solveaxb (A, B, ierr, ndim)
	Solves the linear equation system A*x = B. More...
subroutine	solveeigenvaluea (A, lambda, Z, n, nVal, nVec, ierr)
	Solves a symmetric-definite eigenvalue problem. More...
subroutine	solveeigenvalueb (A, B, lambda, Z, n, nVal, nVec, ierr)
	Solves a generalized symmetric-definite eigenvalue problem. More...

Detailed Description

Module with subroutines for solution of dense linear equation systems.

This module contains subroutines for solving dense linear systems of equations, by wrapping subroutines from the LAPACK linear algebra package.

Function/Subroutine Documentation

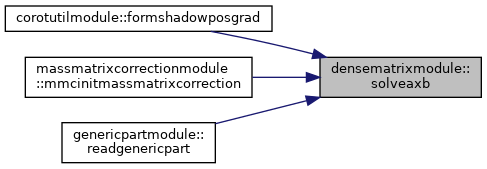
solveaxb()

subroutine densematrixmodule::solveaxb	(	real(dp), dimension(:,:), intent(inout)	A,
		real(dp), dimension(:,:), intent(inout)	B,
		integer, intent(out)	ierr,
		integer, intent(in), optional	ndim
	)

Solves the linear equation system A*x = B.

Parameters

	A	Dense coefficient matrix
	B	Right-hand-side vectors on input, solution vectors on output
[out]	ierr	Error flag
[in]	ndim	Dimension of equation system, specify only if less than size(A,1)

Author

Knut Morten Okstad

Date

21 Jan 2004

Here is the caller graph for this function:

solveeigenvaluea()

subroutine densematrixmodule::solveeigenvaluea	(	real(dp), dimension(:,:), intent(inout)	A,
		real(dp), dimension(:), intent(out)	lambda,
		real(dp), dimension(:,:), intent(out)	Z,
		integer, intent(in)	n,
		integer, intent(in)	nVal,
		integer, intent(in)	nVec,
		integer, intent(out)	ierr
	)

Solves a symmetric-definite eigenvalue problem.

Parameters

	A	Dense coefficient matrix
[out]	lambda	Computed eigenvalues
[out]	Z	Computed eigenvectors
[in]	n	Dimension of the eigenvalue problem
[in]	nVal	Number of eigenvalues to solve for
[in]	nVec	Number of eigenvectors to solve for
[out]	ierr	Error flag

The eigenvalues and (optionally) the associated eigenvectors of the symmetric-definite eigenproblem A*x - λx = 0 is computed using LAPACK::DSYEVX, where A is a dense symmetric matrix.

Author

Knut Morten Okstad

Date

5 Jul 2021

Here is the caller graph for this function:

solveeigenvalueb()

subroutine densematrixmodule::solveeigenvalueb	(	real(dp), dimension(:,:), intent(inout)	A,
		real(dp), dimension(:,:), intent(inout)	B,
		real(dp), dimension(:), intent(out)	lambda,
		real(dp), dimension(:,:), intent(out), target	Z,
		integer, intent(in)	n,
		integer, intent(in)	nVal,
		integer, intent(in)	nVec,
		integer, intent(out)	ierr
	)

Solves a generalized symmetric-definite eigenvalue problem.

Parameters

	A	Dense stiffness matrix
	B	Dense or diagonal mass matrix
[out]	lambda	Computed eigenvalues
[out]	Z	Computed eigenvectors
[in]	n	Dimension of the eigenvalue problem
[in]	nVal	Number of eigenvalues to solve for
[in]	nVec	Number of eigenvectors to solve for
[out]	ierr	Error flag

The eigenvalues and (optionally) the associated eigenvectors of the generalized symmetric-definite eigenproblem A*x - λ*B*x = 0 is computed using LAPACK::DSYGVX, where A and B are dense matrices. If B is a diagonal matrix, the eigenvalue problem is transformed into the form A*x - λ*I*x = 0 where I is the identity matrix, and is solved using the LAPACK::DSYEVX subroutine instead.

Author

Knut Morten Okstad

Date

8 Apr 2011