Module with subroutines for solution of linear equation systems. More...

Data Types
interface	cssolve
	Solves the linear system of equations Ax = B. More...

Functions/Subroutines
subroutine, private	cssolvea (iop, iopSing, sysMat, rhs, lpu, ierr, eqnInErr, meqnInErr, tolFactorize, scaleOnSing, neq1)
	Solves the linear system of equations Ax = B. More...

subroutine, private	cssolveb (iop, iopSing, sysMat, rhs, nrhs, lpu, ierr, eqnInErr, meqnInErr, tolFactorize, scaleOnSing, neq1)
	Solves the linear system of equations Ax = B. More...

subroutine	cssolvesupel (iopSing, sysMat, sysRhs, supElMat, supElRhs, meqn1, meqn2, nrhs, lpu, ierr, Bmatrix, eqnInErr, meqnInErr, tolFactorize, scaleOnSing)
	Performs the superelement reduction for the equation system. More...

subroutine	cslanczoseigensolve (aMat, bMat, mip, mop, meqn1, neq, nEigVal, nEigVec, tolerance, shift, eigValues, eigVectors, ipsw, lpu, meqnInErr, ierr)
	Solves the eigenvalue problem (A + λB) * u = 0. More...

subroutine	csexpand (samData, sveq, svdof, S1, S2)
	Expands and rearranges a solution vector. More...

Variables
real(dp), parameter, private	epsilon_p = 1.0e-12_dp
	Default tolerance. More...

Detailed Description

Module with subroutines for solution of linear equation systems.

This module contains subroutines for solving the linear system of equations that arise in Fedem solver applications. This includes both direct solution for a set of right-hand-side vectors, the reduction of a system of equations such that only external DOFs are retained, as well as eigenvalue solutions. The module defines an interface between the Fedem solver applications and the various 3rd-party linear algebra packages that are being used.

Function/Subroutine Documentation

◆ csexpand()

subroutine solextensionmodule::csexpand	(	type(samtype), intent(in)	samData,
		real(dp), dimension(:), intent(in)	sveq,
		real(dp), dimension(:), intent(out)	svdof,
		real(dp), intent(in), optional	S1,
		real(dp), intent(in), optional	S2
	)

Expands and rearranges a solution vector.

Parameters

[in]	samData	Assembly management data
[in]	sveq	Solution vector expressed in equation order
[out]	svdof	Solution vector expressed in nodal point DOF order
[in]	S1	Scaling factor for the free DOFs (default 1.0)
[in]	S2	Scaling factor for the specified DOFs (default equal to S1)

This subroutine expands and rearranges a system vector expressed in equation order, into a vector corresponding to nodal point order.

Author: Karl Erik Thoresen

Date: Sep 1999

Author: Knut Morten Okstad

Date: Jul 2001

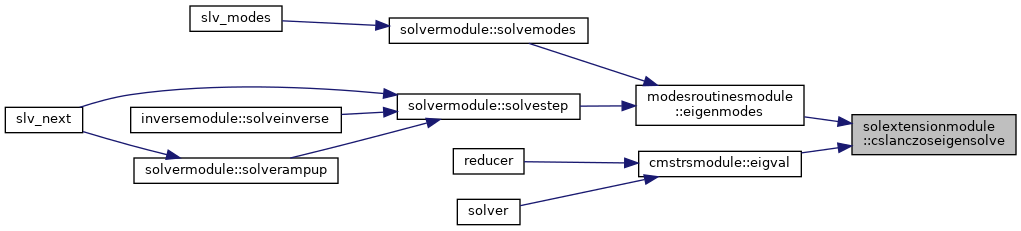
◆ cslanczoseigensolve()

subroutine solextensionmodule::cslanczoseigensolve	(	type(sysmatrixtype), intent(inout)	aMat,
		type(sysmatrixtype), intent(inout)	bMat,
		integer, dimension(:), intent(in)	mip,
		integer, dimension(:), intent(out)	mop,
		integer, dimension(:), intent(in)	meqn1,
		integer, intent(in)	neq,
		integer, intent(in)	nEigVal,
		integer, intent(in)	nEigVec,
		real(dp), dimension(3), intent(inout)	tolerance,
		real(dp), intent(in)	shift,
		real(dp), dimension(:), intent(out)	eigValues,
		real(dp), dimension(:,:), intent(out)	eigVectors,
		integer, intent(in)	ipsw,
		integer, intent(in)	lpu,
		integer(ik), dimension(:), intent(out)	meqnInErr,
		integer, intent(out)	ierr
	)

Solves the eigenvalue problem (A + λB) * u = 0.

Parameters

	aMat	System matrix A
	bMat	System matrix B
[in]	mip	Matrix of input parameters, see LANCZ2 or SPRLAN in SAM
[out]	mop	Matrix of output parameters, see LANCZ2 or SPRLAN
[in]	meqn1	Matrix of status 1 (internal) equation numbers
[in]	neq	Size of the equation system to solve
[in]	nEigVal	Number of eigenvalues to return
[in]	nEigVec	Number of eigenvectors to return
[in]	tolerance	Array of tolerances, see LANCZ2 or SPRLAN
[in]	shift	Shift value
[out]	eigValues	Computed eigenvalues
[out]	eigVectors	Computed eigenvectors
[in]	ipsw	Print switch for debug output
[in]	lpu	File unit number for res-file output
[out]	meqnInErr	Equation numbers of all singularities detected
[out]	ierr	Error flag

Author: Bjorn Haugen

Date: Oct 1998

Author: Knut Morten Okstad

Date: Jan 2003

Here is the caller graph for this function:

◆ cssolvea()

subroutine, private solextensionmodule::cssolvea	(	integer, intent(in)	iop,
		integer, intent(in)	iopSing,
		type(sysmatrixtype), intent(inout)	sysMat,
		real(dp), dimension(:,:), intent(inout)	rhs,
		integer, intent(in)	lpu,
		integer, intent(out)	ierr,
		integer(ik), intent(out), optional	eqnInErr,
		integer(ik), dimension(:), intent(out), optional	meqnInErr,
		real(dp), intent(in), optional	tolFactorize,
		real(dp), intent(in), optional	scaleOnSing,
		integer, intent(in), optional	neq1
	)

private

Solves the linear system of equations Ax = B.

This version accepts the right-hand-side vectors rhs to be provided as a 2D neq×nrhs matrix instead of a 1D array.

See also: solextensionmodule::cssolveb for detailed parameter description

◆ cssolveb()

subroutine, private solextensionmodule::cssolveb	(	integer, intent(in)	iop,
		integer, intent(in)	iopSing,
		type(sysmatrixtype), intent(inout)	sysMat,
		real(dp), dimension(:), intent(inout)	rhs,
		integer, intent(in)	nrhs,
		integer, intent(in)	lpu,
		integer, intent(out)	ierr,
		integer(ik), intent(out), optional	eqnInErr,
		integer(ik), dimension(:), intent(out), optional	meqnInErr,
		real(dp), intent(in), optional	tolFactorize,
		real(dp), intent(in), optional	scaleOnSing,
		integer, intent(in), optional	neq1
	)

private

Solves the linear system of equations Ax = B.

Parameters

[in]	iop	Calculation option (see below)
[in]	iopSing	Singularity handling options (see below)
	sysMat	The coefficient matrix A
	rhs	The right-hand-side vector(s) B, solution on output
[in]	nrhs	Number of right-hand-side vectors
[in]	lpu	File unit number for res-file output
[out]	ierr	Error flag
[out]	eqnInErr	Equation number of the first singularity detected
[out]	meqnInErr	Equation numbers of all singularities detected
[in]	tolFactorize	Singularity tolerance
[in]	scaleOnSing	Scaling factor for singular pivot elements
[in]	neq1	Number of equations to solve for

Basic equations: Ax = B, LDL'x = B, LDy = B, L'x = y. The value on the input argument iop defines which solution step to do:

= 1 : Factorization (compute L and D in A = LDL')
= 2 : Factorization and forward reduction (compute L and D in A = LDL' and y in LDy = B)
= 3 : Factorization, forward reduction and back substitution (compute L and D in A = LDL', y in LDy = B and x in L'x = y)
= 4 : Forward reduction and back substitution (compute y in LDy = B and x in L'x = y)
= 5 : Forward reduction only (compute y in LDy = B)
= 6 : Back substitution only (compute x in L'x = y)

The singularity handling flag iopSing is interpreted as follows:

> 1 : Do a solve with modified matrix to override singularities
= 1 : Same as for > 1, but override only the true singularities
= 0 : Abort if the matrix is singular
< 0 : Same as for > 0, but suppress all the singular equations

Author: Bjorn Haugen

Date: Sep 1998

Author: Knut Morten Okstad

Date: Jan 2003

◆ cssolvesupel()

subroutine solextensionmodule::cssolvesupel	(	integer, intent(in)	iopSing,
		type(sysmatrixtype), intent(inout)	sysMat,
		real(dp), dimension(:,:), intent(in)	sysRhs,
		real(dp), dimension(:,:), intent(out)	supElMat,
		real(dp), dimension(:,:), intent(out), target	supElRhs,
		integer, dimension(:), intent(in)	meqn1,
		integer, dimension(:), intent(in)	meqn2,
		integer, intent(in)	nrhs,
		integer, intent(in)	lpu,
		integer, intent(out)	ierr,
		type(diskmatrixtype), intent(inout), optional	Bmatrix,
		integer(ik), intent(out), optional	eqnInErr,
		integer(ik), dimension(:), intent(out), optional	meqnInErr,
		real(dp), intent(in), optional	tolFactorize,
		real(dp), intent(in), optional	scaleOnSing
	)

Performs the superelement reduction for the equation system.

Parameters

[in]	iopSing	Singularity handling options (see below)
	sysMat	The system stiffness matrix
[in]	sysRhs	The system right-hand-side vector(s)
[out]	supElMat	The reduced stiffness matrix, K
[out]	supElRhs	The reduced right-hand-side vector(s), f
[in]	meqn1	Matrix of status 1 (internal) equation numbers
[in]	meqn2	Matrix of status 2 (external) equation numbers
[in]	nrhs	Number of right-hand-side vectors
[in]	lpu	File unit number for res-file output
[out]	ierr	Error flag
[out]	Bmatrix	Displacement recovery matrix
[out]	eqnInErr	Equation number of the first singularity detected
[out]	meqnInErr	Equation numbers of all singularities detected
[in]	tolFactorize	Singularity tolerance
[in]	scaleOnSing	Scaling factor for singular pivot elements

A static condensation of the internal (i) degrees of freedom is performed, retaining only the external (e) degrees of freedom, i.e.,

    |Kii Kie|*|vi| = |fi|    ====>   K*ve = f
    |Kei Kee| |ve|   |fe|
     (sysMat)      (sysRhs)

where

    K = Kee - Kei*(Kii^-1)*Kie    (returned in supElMat)
    f = fe  - Kei*(Kii^-1)*fi     (returned in supElRhs)

If the Bmatrix is present, it is also returned

    B = -(Kii^-1)*Kie

The singularity handling flag iopSing is interpreted as follows:

> 1 : Do a solve with modified matrix to override singularities
= 1 : Same as for > 1, but override only the true singularities
= 0 : Abort if the matrix is singular

Author: Bjorn Haugen

Date: Nov 1998

Author: Knut Morten Okstad

Date: Jan 2003

Here is the caller graph for this function:

Variable Documentation

◆ epsilon_p

real(dp), parameter, private solextensionmodule::epsilon_p = 1.0e-12_dp

private

Default tolerance.

Data Types

Functions/Subroutines

Variables

Detailed Description

Function/Subroutine Documentation

◆ csexpand()

◆ cslanczoseigensolve()

◆ cssolvea()

◆ cssolveb()

◆ cssolvesupel()

Variable Documentation

◆ epsilon_p